DFS III

The main characteristics of DFS is going back to where it is from (Back Tracking).
What should be kept in mind is how many times it excuted, and what is the status of each execution.

Article Language: English
Example Language: Java
Reading Time: 5min

Different from the type of subset, which usually starts from ‘empty’, and decided whether choose and continue from a node, while the type of permutation questions requires every single elements appears to the result. The result is determined by order. It can be started from ‘empty’, then only the last execution gives the valid result. Otherwise, every permuation needs to be added to the result. The principle is making every elements showing on every position.

Permutation

input: A linear data structure like an array, a string, etc. No duplicated element.
output: A list of lists of all permutations.

• It needs to try every position for every single element. And it has number of n choices for each position.
• It has number of n - i choices on the i-th position.
• The most important is using control statement (for-loop here) to decide layer instead of status.
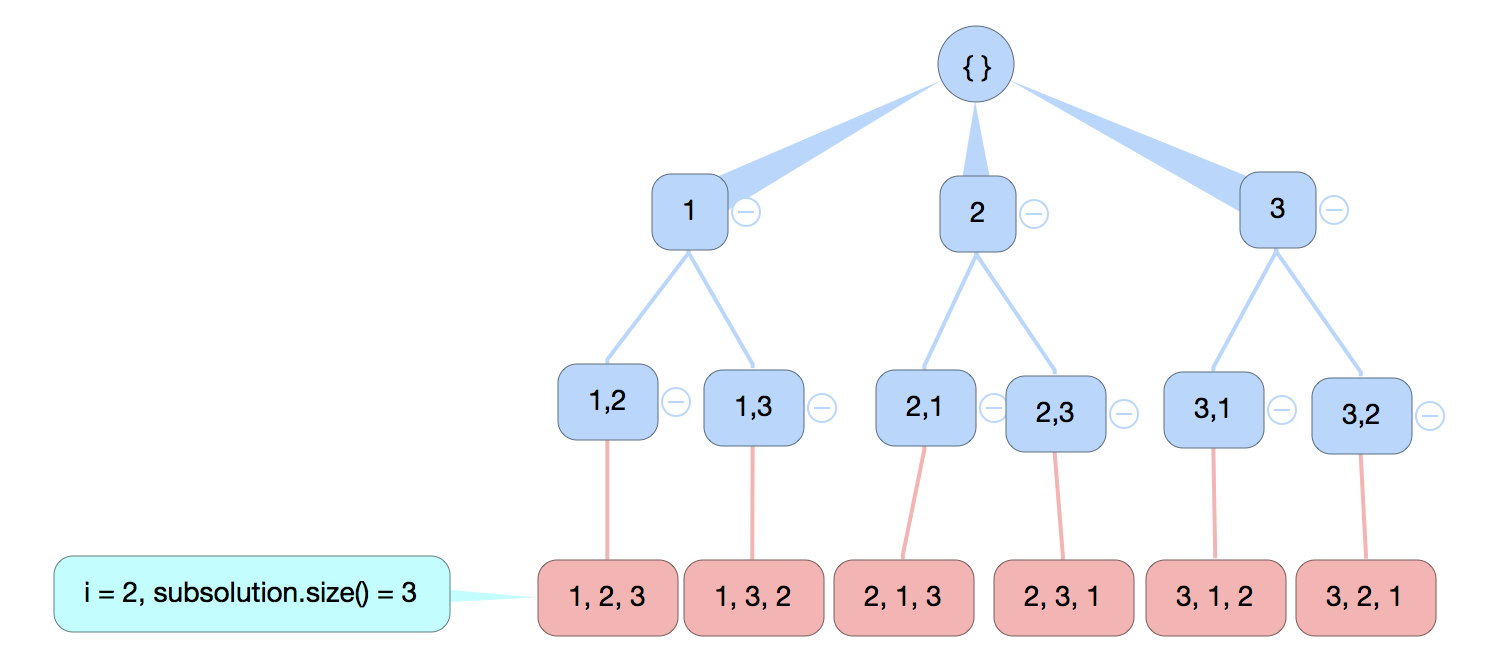
  For each position i, it has at most (n - i) - i choices, where i represents the level of the node. Therefore, the time complexity would be O(n!).
  This case chooses to use a boolean array to indicate the elements that has appeared in the subsolution. This costs O(n). And the depth of the recursive call would be n, so the call stack would take O(n). Thus, the space would be O(2n) ==> O(n).

public class Permutation {
	public List<List<Integer>> permutation(int[] input) {
		if (input == null) {
			return new ArrayList<>();
		}

		List<List<Integer>> result = new ArrayList<>();
		dfs(input, new HashSet<>(), new ArrayList<>(), result);
		return result;
	}

	private void dfs(int[] input,
			Set<Integer> occ,
			List<Integer> sub,
			List<List<Integer>> result) {
		if (sub.size() == input.length) {
			result.add(new ArrayList<>(sub));
			return;
		}

		for (int i = 0; i < input.length; i++) {
			if (occ.contains(input[i])) {
				continue;
			}
			sub.add(input[i]);
			occ[i] = true;
			dfs(input, occ, sub, result);
			sub.remove(sub.size() - 1);
			occ[i] = false;
		}
	}
}

Optimize: Additional data strucutre for estimating elements in current execution is not necessary, ❤~

---

Permutation II

input: A linear data structure like an array, a string, etc. With DUPLICATED elements.
output: A list of lists of all UNIQUE permutations.

• It whether exists duplicated elements, how to dedup?
• Similar to SubsetII with duplicated elements.
• It needs to know whether current element is being used, so a HashSet maybe helpful.
• Do not continue if current element is being used.

At each position i, it has n - i times choices, as same as the regular permutation.
A HashSet is used to deduplicate. At each level i, at most n - i space would be taken to save visited element. Space complexity would be n + (n - 1) + (n - 2) + (n - 3) + …. + 2 + 1 = O (n^2).

public class Permutation {
	public List<List<Integer>> permutation(int[] input) {
		if (input == null) {
			return new ArrayList<>();
		}

		List<List<Integer>> result = new ArrayList<>();
		//dfs(input, new HashSet<>(), new ArrayList<>(), result);
		dfs(input, new ArrayList<>(), result)
		return result;
	}

	private void dfs(int[] input,
		/*Set<Integer> occ,*/
		List<Integer> sub,
		List<List<Integer>> result) {
		if (sub.size() == input.length) {
			result.add(new ArrayList<>(sub));
			return;
		}

		Set<Integer> occ = new HashSet<>();
		for (int i = 0; i < input.length; i++) {
			if (occ.contains(input[i])) {
				continue;
			}
			sub.add(input[i]);
			occ[i] = true;
			dfs(input, occ, sub, result);
			sub.remove(sub.size() - 1);
			occ[i] = false;
		}
	}
}