Binary Search

Posted on | Edited on | In | | Views:

Binary search is a search algorithm. The fundamental is that it reduces the searching range into half each time by comparing the middle element to the target. Normal binary search takes O(logn) comparisons, when n is the number of input. Space actually depends on the implementation. If not using recursion, there would be no extra space used in a regular binary search. Therefore, it normally is O(1).

Article Language: English
Example Language: Java
Reading Time: 17min

Key concept:

  1. Input must be in some sort of order (ascending, descending, alphabetic, positve and nagative, increased then descrease, etc.)
  2. Searching/calculation/operating range must be reduced each time.
  3. Targe must not be ruled out.

input: A sorted array and a target.
output: Index of the target if exits, otherwise, return -1;

Iteration
Time complexity is O(logn), where n is the size of input. Space is O(1) using iteration.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public class BinarySearch {
    /**
     * @param array
     * @param target
     * @return
     */
    public int binarySearch (int[] array, int target) {
        if (array == null || array.length == 0) return -1;
        int left = 0, right = array.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (array[mid] == target) {
                return mid;
            }
            //other wise mid is not the result, rule it out.
            if (array[mid] > target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        //if not return in the while loop, target doesn't exist.
        return -1;
    }
}

Recursion
Time complexity is the same as O(logn). Call stack counts as space expense, which is O(logn).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public class BinarySearch {
    /**
     * @param array
     * @param target
     * @return
     */
    public int binarySearch (int[] array, int target) {
        if (array == null || array.length == 0) return -1;

        return helper(array, 0, array.length - 1, target);
    }

    private int helper(int[] array, int left, int right, int target) {
        if (left > right) return -1;

        int mid = left + (right - left) / 2;
        if (array[mid] == target) return mid;
        //if not return, mid is not target, can rule out mid.
        if (array[mid] > target) {
            return helper(array, left, mid - 1, target);
        } else {
            return helper(array, mid + 1, right, target);
        }
    }
}

Search a 2D Matrix I

input: A matrix that each row is in ascending order, and the first element of each row is greater than the last element of previous row. A int type target.
output: The coordinate of the target if exists. Otherwise, return -1.

One way to solve this problem by using binary search is convert 2D matrix into an array. Due to the property of the matrix, from left to right, top to buttom, all elements are in ascending order. Therefore, it will be able to use the classic binary search. The time complexity is O(n + m) where n is the number of row and m is the number of colmun. Space complexity is O(1). No extra data structure is used.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public class Search2DMatrix {
    /**
     * @param matrix
     * @param target
     * @return
     */
    public int searchMatrixI (int[][] matrix, int target) {
        if (matrix == null || matrix.length == 0 || matrix[0] == null || matrix[0].length == 0) return -1;

        int row = matrix.length;
        int column = matrix[0].length;

        int left = 0, right = row * column - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            int x = mid / column, y = mid % column;
            if (matrix[x][y] == target) {
                return matrix[x][y];
            }
            if (matrix[x][y] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return -1;
    }
}

Search in a Unknown Size Array

input: An unknwon size array in ascending order, you can only access the kth number by ArrayReader.get(k). A target number.
output: return the first occurrence of the target.

Only thing differnce from classic bianry search is right boundary. While checking the right boundary, set the left boundary where is the last position that the element is smaller than the target. Jumping 2 times of the current element to locate the right boundary, then the time complexity is O(logk + O(logn)) where k is the element from the left boundary to the right boundary, n is the number of elements preceding the left boundary.
The only reason jumping 2 times instead of a larger one is beacuse the final time complexity is difference only in coefficient. The size is unknwon. If there are only a few of elements in the array, jumping 10 times or 20 times would be out of bounds. It is not worth to take the risk.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public class SearchUnknownSize {
    /**
     * @param reader: An instance of ArrayReader.
     * @param target: An integer
     * @return: An integer which is the first index of target.
     */
    public int searchBigSortedArray(ArrayReader reader, int target) {
        if (reader == null) {
            return -1;
        }
        //locate right boundary
        int right = 1;
        int left = 0;
        while (reader.get(right - 1) < target) {
            right *= 2;
            left = right;
        }
        //binary search for first occurrence
        while (left + 1 < right) {
            int mid = left + (right - left) / 2;
            if (reader.get(mid) >= target) {
                right = mid;
            } else if (reader.get(mid) < target) {
                left = mid + 1;
            }
        }

        if (reader.get(left) == target) return left;
        if (reader.get(right) == target) return right;
        return -1;
    }
}

First Bad Log

The concept is using binary search to find the left and right boundary, and locate the first occurrence of the bad log.

Search Insert Position

input: an integer array and a target number.
output: return the index if the target is found. If not, return the index where it would be if it were inserted in order.

It is easier to find a closest number to the target, then compare the element to the target,

  1. insert target at the position it if the element is greater or equal to the target.
  2. insert target after the position if the element is smaller than the target.

The time comlexity is O(logn). Space complexity is O(1).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public class searchInsert {
    /**
     * @param input: an integer sorted array
     * @param target: an integer to be inserted
     * @return: An integer
     */
    public int searchInsert(int[] input, int target) {
        // write your code here
        if (input == null || input.length == 0) {
            return 0;
        }

        int left = 0;
        int right = input.length - 1;

        //keep one element for comparing to the target.
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (input[mid] >= target) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }

        if (input[left] >= target) {
            return left;
        }

        return left + 1;
    }
}

First Occurrence of Target

input: an sorted int array in ascending order
output: index of the first occrrence of the target. If not exist, return -1;
I’d like call it look to the left. Using binary search, if greater or equal, set the right boundary at the position. If less than the target, the element is excluded from searching range.
Time comlexity is O(logn), space is O(1).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public class FirstOccurrence {
    /**
     * @param input
     * @param target
     * @return first occurrence of the target
     */
    public int firstOccurrence(int[] input, int target) {
        if (input == null) return -1;

        int left = 0, right = input.length - 1;
        while (left + 1 < right) {
            int mid = left + (right - left) / 2;
            if (input[mid] >= target) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        if (input[left] == target) return left;
        return right;
    }
}

Last Occurrence of Target

input: an sorted int array in ascending order
output: index of the last occurrence of the target. If not exisit, return -1.

I’d like call it look to the right. Similar to first occurrance. Only difference is if the element at the middle is less than or equal to the target, set the left boundary, because right result must be in the range from the position to the end. If the middle element is greater than the target, it is eliminated from the result.

Time comlexity is O(logn), space is O(1).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public class LastOccurrence {
    /**
     * @param input
     * @param target
     * @return first occurrence of the target
     */
    public int lastOccurrence(int[] input, int target) {
        if (input == null) return -1;

        int left = 0, right = input.length - 1;
        while (left + 1 < right) {
            int mid = left + (right - left) / 2;
            if (input[mid] <= target) {
                left = mid;
            } else {
                right = mid - 1;
            }
        }
        if (input[right] == target) return right;
        return left;
    }
}

Total Occurrence of Target

input: an int array in ascending order and a target number.
output: return the total occurrence of the target.

One way to do it is, targeting either the first occurrence or the last occurrence of the target. The look throught it and count. The time complexity would be O(logn) for finding the position and O(k) for looping the number of target, so it is O(logn + k). Space comlexity is O(1).

Another way of calculating the number of target in the array is to get both first occurrence and the last occurrence of the larget. Using the last position minus the first position and plus 1 to get the total number of target in the array. The time complexity is O(2logn). Space Comlextiy is O(1).

Which ways is bettern actually depending on the number of target, k. If all elements in the array are the same numbers. For example, {1, 1, 1, …, 1, 1}. The first method becomes O(n). The second method remains the same. However, if k is a really small number, then the first method is better.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public class TotalOccurrence {
    /**
     * @param input:  an integer array sorted in ascending order
     * @param target: An integer
     * @return: An integer
     */
    public int totalOccurrence(int[] input, int target) {
        if (input == null ||
                input.length == 0 ||
                input[0] > target ||
                input[input.length - 1] < target) {
            return 0;
        }

        int left = 0, right = input.length - 1;
        //left boundary
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (input[mid] >= target) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        //退出条件是一个元素, 如果不等于 target, 则 target 不存在.
        if (input[left] != target) return 0;

        //left boundary and right boundary
        int start = left, end = input.length - 1;

        //right boundary
        right = end;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (input[mid] <= target) {
                left = mid + 1;
                end = mid;
            } else {
                right = mid - 1;
            }
        }
        return end - start + 1;
    }
}

Search for a Range

As same as total occurance, only changes the return type to a new int[]{start, end}.
Time and space comlexity are the same, too.

Closest Number to Target

input: An integer array and an integer target number.
output: return the number that closest to the target.

Time complexity is O(logn). Space complexity is O(1). Using binary search and reducing the candidate to two elements. Whichever closer to target is the result.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public class ClosestNumber {
    /**
     * @param input an integer array sorted in ascending order
     * @param target an integer
     * @return an integer
     */
    public int closestNumber(int[] input, int target) {
        if (input == null || input.length == 0) {
            return -1;
        }

        int left = 0, right = input.length - 1;
        while (left + 1 < right) {
            int mid = left + (right - left) / 2;
            if (input[mid] <= target) {
                left = mid;
            } else {
                right = mid;
            }
        }

      return Math.abs(input[left] - target) < Math.abs(input[right] - target) ? left : right;
    }
}

Search in Rotated Sorted Array I

input: a sorted array is rotated at some unknown pivot and a target number. (No duplicates)
output: return the index of target if exists. Otherwise, return -1.

Since the array is still sorted in a way, it still can use binary search. The middle element has 3 situations:

  1. it is the target
  2. it is in an rotated interval (greater than the right most element)
    • it is greater than the target, target could be in both side of the array.
    • it is less than target, set the left boundary.
  3. it is in an unrotated interval (smaller than the right most element) - it is greater than the target, set the right boundary. - it is less than the target, target could be in both side of the array.
    This problem actually would be more straitforwar if looking at a picture.

The time complexity is as same as classic binary search, O(logn), although it has more conditions. Space complexity is O(1).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public class RoatedSortedArrayI {
    /**
     * @param input
     * @param target
     * @return
     */
    public int search(int[] input, int target) {
        if (input == null || input.length == 0) {
            return -1;
        }

        int left = 0, right = input.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;

            if (input[mid] == target) {
                return mid;
            }
            //第一个上升区间
            if (input[mid] > input[right]) {
                if (input[mid] > target && target > input[right]) {
                    right = mid - 1;
                } else {
                    left = mid + 1;
                }
            }
            //第二个上升区间
            if (input[mid] < input[left]) {
                if (input[mid] < target && target < input[left]) {
                    left = mid + 1;
                } else {
                    right = mid - 1;
                }
            }
        }
        return -1;
    }
}

Search in Rotated Sorted Array II

input: rotated array with duplicates.
output: index of target.

Fist of all, run a for loop searching target takes O(n). If the array is rotated with duplicates, it takes redundant checks to determine whether the middle point is in which interval. For example, {1, 1, 1, 1, 1, 0, 1, 1, 1}. The time complexity would be O(n) the worst case. Therefore, just simply run a loop.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class SearchRotateArrayII {
    /**
     * @param input: an integer ratated sorted array and duplicates are allowed
     * @param target: An integer
     * @return: index
     */
    public int search(int[] input, int target) {

        if (input == null) {
            return -1;
        }

        for (int i = 0; i < input.length; i++) {
            if (input[i] == target) {
                return i;
            }
        }

        return -1;
    }
}

Find Peak Element

input: An integers array that the numbers in adjacent positions are different. A[0] < A[1] && A[A.length - 2] > A[A.length - 1].

Peak in an array: A[P] > A[P-1] && A[P] > A[P+1] > output: return any of peek positions. There might be more than one peeks.

According to the definition of the peek and the array’s feature. Returning any peek can use a binary saerch. Since the array is kind of sorted, the middle point would have three situations.

  1. middle point is the peek
  2. middle point is in the left side of a peek, then it’s in ascending order (like going uphill)
  3. middle point is in the right side of a peek, then it’s in descending order (like going downhill)

Time comlexity is O(logn). Space complexity is O(1).

If using ‘left + 1 < right’ as the condition of the while loop, it eliminates many checkings for index out of bounds excemption. The element always needs to compare with its neighbor, so it’s easier to keep at least three elements during the comparing. Making sure that the peek would not be ruled out guarantees the greater element to be the peek when finishing the loop.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public class FindPeek {
    /**
     * @param input: An integers array.
     * @return: return any of peek positions.
     */
    public int findPeak(int[] input) {
        if (input == null || input.length < 3) {
            return -1;
        }

        int left = 0, right = input.length - 1;
        while (left + 1 < right) {
            int mid = left + (right - left) / 2;
            /*if (input[mid] > input[mid - 1] && input[mid] > input[mid + 1]) {
                return mid;
            }*/
            //at ascending interval
            if (input[mid] > input[mid - 1]) {
                left = mid;
            }
            //at descending interval
            if (input[mid] < input[mid - 1]) {
                right = mid;
            }
        }
        if (input[left] > input[right]) {
            return left;
        }
        return right;
    }
}

Maximum Number in Mountain Sequence

input: An integer array which increase firsly and then decreses.
output: return the mountain top.

Actually the same question as find peek. T = O(logn), S = O(1). Comparing an element to its neighbor is always easier to keep at least 3 elements. It saves many index boundary check. Notice that left or right boundary could be the candidate of the result, it should not be eliminated.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public class MountainTop {
    /*
     * @param input: a mountain sequence which increase firstly and then decrease
     * @return: then mountain top
     */
    public int mountainSequence(int[] input) {

        if (input == null || input.length == 0) {
            return 0;
        }

        int left = 0, right = input.length - 1;

        while (left + 1 < right) {
            int mid = left + (right - left) / 2;

            if (input[mid] < input[mid + 1]) {
                left = mid;
            } else {
                right = mid;
            }
        }
        return Math.max(input[left], input[right]);
    }
}

Find Minimum in Rotated orted Array I

This question is actually as same as finding the peek.

Find Minimum in Rotated orted Array II

As same as duplicates in a rotated sorted array, it is not worth to use binary search with all redundant checks.

Single Number IV

input: an int array with all the numbers appear twice except one number which appears once and all the numbers which appear twice are next to each other.
output: find the number that appears once. 找出单身狗 🤣

Intuitive way is using a set. Beacuse of the property of set, if there exisit the element, remove the element. The one left in the set would be the result. Time comlexity is O(n), and space complexity is about O(n) during the comparing. However, this would waste the clue that “same numbers appear next to each other”. Since the intutitive way takes only O(n), optimized method ought to be better than that.

Since there is only 1 missing number, then the number element of the input must be odd.
There are 2 cases of the middle number.

  1. the middle number is the missing number.
  2. the middle number has an ajacent duplicate number.
    • The adjacent number with the same value is in the left side.
    • the adjacent number with the same value is in the right side.


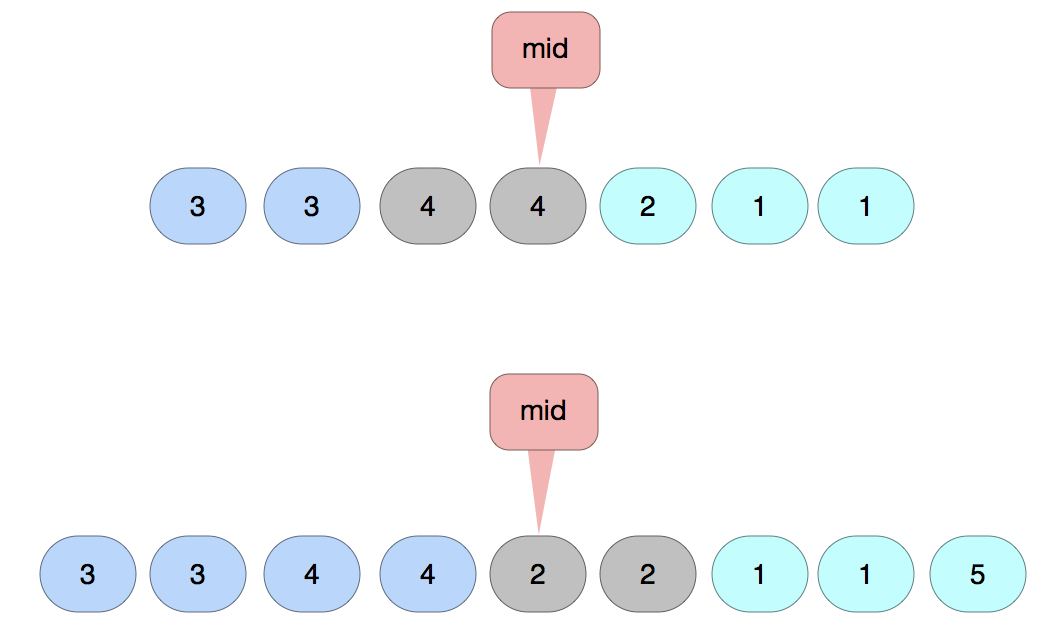
The key point is, the side that has the odd number of element after eliminating the middle pair has the missing number. Time comlexity is O(logn). Space comlexity is O(1).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public class MissingNumberIV {
    /**
     * @param nums
     * @return the lonely number
     */
    public int getSingleNumber(int[] nums) {
        if (nums == null || nums.length == 0 || nums.length % 2 == 0) return -1;
        if (nums.length == 1) return nums[0];

        //if not return, the array has at lest 3 elements.
        int left = 0, right = nums.length - 1;

        while (left < right) {
            int mid = left + (right - left) / 2;

            //和右边相等的话, 右边减去1 是不是偶数
            if (nums[mid] == nums[mid + 1]) {
                if ((right - mid - 1) % 2 == 0) {
                    right = mid - 1;
                } else {
                    left = mid + 2;
                }
            } else if (nums[mid] == nums[mid - 1]) {
                if ((mid - left - 1) % 2 == 0) {
                    left = mid + 1;
                } else {
                    right = mid - 2;
                }
            } else {
                return nums[mid];
            }
        }
        return nums[left];///
    }
}

Power(x, n)

input: two integers.
output: return the power of the first number.

There are several cases need to concern in the arithmetical opeation:

  1. overflow
  2. base is 0
    • if exponent <= 0, error
    • if exponent > 0, return 0
  3. exponent is 0, return 1
  4. exponent is negative, 1 / result
  5. exponent is positive,
    • exponent is even number
    • exponent is odd number

Using recursion to reduce the power. a to the power of b can be divided into a to the half of power of b times a to the half of power of b. And so on and so forth. The complexity is O(logb). Space compexity is O(logb) due to the call stack.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public class PowerAB {
    /**
     * @param a
     * @param b
     * @return
     */
    public double power (int a, int b) {
        if (a == 0) {
            if (b <= 0) {
                throw new IllegalArgumentException("Illegal input");
            }
            return 0;
        }
        if (b < 0) {
            return 1 / helper(a, -b);
        }
        return helper(a, b);
    }

    private double helper(int a, int b) {
        if (b == 0) {
            return 1;
        }
        double half = helper(a, b / 2);
        if (b % 2 == 0) {
            return half * half;
        }
        return half * half * a;
    }
}

Divide Two Integers

input: two itnegers
output: divide two integers without using multiplications, division and modulo.

Using divisor to reduce the number of dividend to get the result. Counting how many dividend has been detracted1. Similar as doing power of two integers, using binary concept to accelerate the process2. Time complexity is O(logn) where n is the divisor and the space complexity is O(1).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
public class DivideTwoIntegers {
    /**
     * @param dividend
     * @param divisor
     * @return
     */
    public int divide(int dividend, int divisor) {
        if (dividend == 0) {
            throw new IllegalArgumentException("Dividend cannot be 0.");
        }

        if (divisor == 0) {
            return dividend < 0 ? Integer.MIN_VALUE : 0;
        }

        if (dividend == Integer.MIN_VALUE && divisor == -1) {
            return Integer.MAX_VALUE;
        }

        boolean isNegative = (dividend < 0 && divisor > 0 ||
                              dividend > 0 && divisor < 0);

        long absDividend = Math.abs((long) dividend);
        long absDivisor = Math.abs((long) divisor);

        long result = 0;

        while (absDividend >= absDivisor) {
            int shift = 0;
            while (absDividend >= (divisor << shift)) {
                shift++;
            }
            dividend -= divisor << (shift - 1);
            result += 1 << (shift - 1);
        }

        return isNegative ? (int) -result : (int) result;
    }
}

Find Smallest Letter Greater Than Target (LeetCode 744)

input: a char array of sorted letters containing only lowercase letters, and given a target letter target.
output: return the smallest element in the list that is larger than the given target.

Letters are ordered is ideal for binary search. Time complexity is O(logn). Space is O(1). Keep one element that is greater than the target. If the characters is less than or equal to target, target must closer to the first element in the array. Otherwise, the character is the result.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class SmallestGreaterLetter {
    /**
     * @param letters
     * @param target
     * @return
     */
    public char nextGreatestLetter(char[] letters, char target) {
        if (letters == null) return ' ';

        int left = 0, right = letters.length - 1;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (letters[mid] <= target) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }

        if (letters[left] <= target) return letters[0];
        return letters[left];
    }
}

<!– ### Count of Smaller Number
input: an integer array and a query list.
output: return the number of element in the array that are smaller than the given number in the query.

続く。

  1. 1.https://blog.csdn.net/fightforyourdream/article/details/16899675 ↩
  2. 2.http://www.cnblogs.com/yuzhangcmu/p/4049170.html ↩