Data Structure VI Graph I

Posted on | Edited on | In | | Views:

A graph is formed by the non-empty set of vertex and set of edge. Use G <E, V> to represent a graph, G, and the sets of it’s vertex, V, and edge, E.

Article Language: English
Example Language: Java
Reading Time: 12min

Undirected Graph

A graph is a set of vertices and a collection of edges that each connect a pair of vertices

Representation of Graph Data Structure (common)

  1. Ajacentcy Matrix: using a 2D array to indicate the relationship between vertex (row) and edge (column). Uses O(n^2) space for a sparse graph, not recommended.
  2. Ajacentcy List:
    • Array of array to represent the relationship between the vertex (index), and the edge (array corresponds to the index). Even though the worst case of space using is still O(n^2), normally is better than ajacentcy matrix.
    • Map<T, Set<T>>, where T is the vertext and Set is the set of edge. (Java)
    • Class of GraphNode, which has two main field, the vertext and the list of its neighbors.(Java)
1
2
3
4
class GraphNode{
	int vertexLabel;
	List<GraphNode> neighbors;
}

Traverse a Graph

input: A graph node, assume that the graph is connected.
output: A list of all nodes’ value in the graph.

Unlike doing BFS on a tree, an extra data structure need to be used in traverse to avoid revisiting a node in a graph. Tree is a directed acyclic graph. If there are n nodes in a tree, there must be n - 1 edges, and every node can be visited from the root. Three main differences,

  1. A graph may or may not have direction. (better breadth first from one vertex)
  2. A graph may have circle. (markvisited)
  3. Nodes in a graph may not be connected. (all nodes must be given unless its connected)

The data structure that widely used in BFS is queue, due to its FIFO property (in the order from left to right in a level). In a graph, node in the queue is the one that is waiting for expending. Meanwhile, set is saving all generated (visited/put in the queue) nodes. To sum, there are two common data structure involved in traversing a graph in general.(Java)
Time complexity is O(v + e), where v is the number of vertex and e is the number of edge. Space is O(v), where v is the number of nodes because the worst case is to save all vertex.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public class Solution{
	class GraphNode{
		int label;
		List<GraphNode> neighbors;
		public GraphNode(int val) {
			label = val;
			neighbors = new ArrayList<GraphNode>();
		}
	}
	//Assume it's a connected graph
	public List<Integer> traverseGraph(GraphNode node) {
		List<Integer> result = new ArrayList<>();
		if (node == null) return result;

		Queue<GraphNode> queue = new LinkedList<>();
		Set<GraphNode> visited = new HashSet<>();
		queue.offer(node);
		visited.add(node);
		while (!queue.isEmpty()) {
			GraphNode cur = queue.poll();
			result.add(cur.label);
			for (GraphNode n : cur.neighbors) {
				if (!visited.contains(n)) {
					visited.add(n);
					queue.offer(n);
				}
			}
		}
		return result;
	}
}

Clone Graph

input: A graph node, if the graph is connected, or a list of all nodes in the graph (easier).
output: Deeped copyed node of new graph, or a list of all nodes that is copied.

Similar to traverse a graph, except two more steps,

  1. Traverse the graph and get all nodes. (if not given)
  2. Copy all vertex(nodes)
  3. Copy all neighbors for every vertex.

An extra data structure Map<GraphNode, GraphNode> is used here for mapping the original and copied node. Neighbors can be copied by tracing the key in the map.

Time complexity is 3 times of traversal because at each step, all nodes need to be visited, so O(3(v + e)) is O(v + e).
Space complexity is 2 times of traversal if list of node is not given. No matter the input form, the space complexity is going to be O(v), where v is the number of vertex.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public GraphNode clone(GraphNode node) {
	if (node == null) return null;
	//get node
	List<GraphNode> list = getNodes(node);

	//copy node, key is the original node, and create a same node as its value.
	Map<GraphNode, GraphNode> map = new HashMap<>();
	for (GraphNode n : list) {
		map.put(n, new Graph(n.label));
	}

	//copy neighbor/edge
	for (GraphNode ver : list) {
		GraphNode newNode = map.get(ver);
		for (GraphNode nei : ver.neighbors) {
			newNode.neighbors.add(map.get(nei));
		}
	}
	return map.get(node);
}

private List<GraphNode> getNodes(GraphNode node) {
	Queue<GraphNode> q = new LinkedList<>();
	Set<GraphNode> visited = new HashSet<>();

	q.offer(node);
	visited.add(node);
	while(!q.isEmpty()) {
		GraphNode cur = q.poll();
		for (GraphNode nei : cur.neighbors) {
			if (!visited.contains(nei)) {
				q.offer(nei);
				visited.add(nei);
			}
		}
	}
	return new ArrayList<>(visited);
}

Sometimes, step/level/layer matters. Which means there needs to be a indicator for nodes that can be expanded from one. Just like BFS in a tree, use current size of the queue to detemine whether the nodes in the same level or not. There are other ways to indicate differnce levels in a graph, like two queues, indicator node, etc. I prefer more general way that can be used in both graph and tree.

Traverse a Graph by Layer

input: A graph node, assume that the graph is connected.
output: A list of list of all nodes’ value in the graph.

Code is pretty similar to regular traversal, only add a for loop to track the number of nodes at the same level.
The time comlexity doesn’t change. It is O(v + e), and the space is O(v) as same as traversal.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public class Solution{
	class GraphNode{
		int label;
		List<GraphNode> neighbors;
		public GraphNode(int val) {
			label = val;
			neighbors = new ArrayList<GraphNode>();
		}
	}
	//Assume it's a connected graph
	public List<List<Integer>> traverseGraph(GraphNode node) {
		List<Integer> result = new ArrayList<>();
		if (node == null) return result;

		Queue<GraphNode> queue = new LinkedList<>();
		Set<GraphNode> visited = new HashSet<>();
		queue.offer(node);
		visited.add(node);
		while (!queue.isEmpty()) {
			//size changes every time generates a node
			int size = queue.size();
			List<GraphNode> level = new ArrayList<>();
			//run loop for current size of the queue
			for (int i = 0; i < size; i++) {
				GraphNode cur = queue.poll();
				level.add(cur.label);
				for (GraphNode n : cur.neighbors) {
					if (!visited.contains(n)) {
						visited.add(n);
						queue.offer(n);
					}
				}
			}
			result.add(level);
		}
		return result;
	}
}

There are more useful way of indicating levels while traversing. For example, find steps from one node to the other. Every level includes one more step towards to the target node.

ShortestPath(monodirection)

input: List of graph node, starting node, and target node. If given graph is not null, both start and end position are not null.
output: Return the shortest path from the start to the target. If there is not such path, return -1.

In an undirected graph, there are many ways to visualize a graph. For example, there is a graph has 10 nodes, and 12 edges, shown in the picture. It can ba organized to,
看这销魂的走位(ง•̀-•́)ง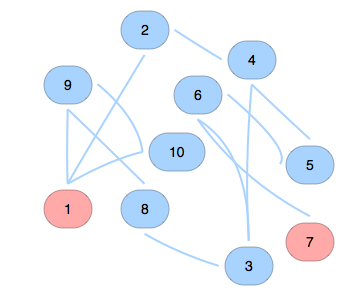

il suffit de prendre un noeud…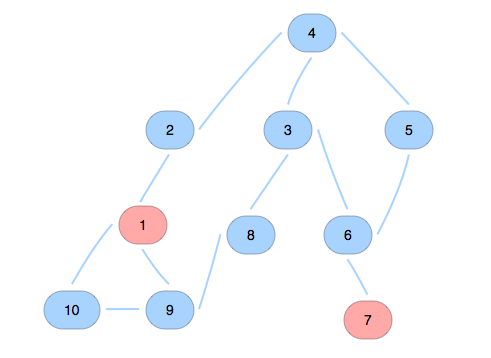

こんなことも〜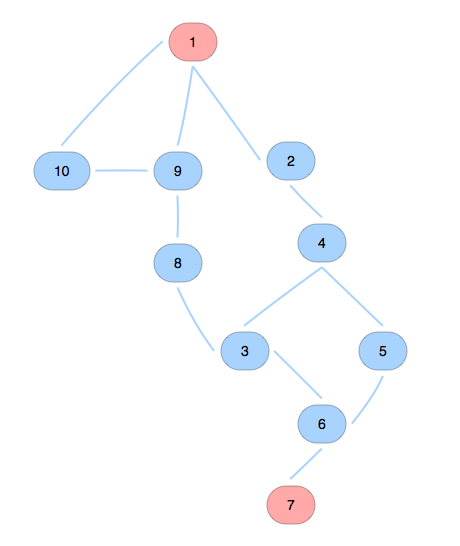

There is always a way to put some node in the same level from a start node as shown in the 2nd and third pictures.

The only thing needs to be considered is how many levels or steps it takes until the target appears in the queue, then it is the final step to reach the target.
Time comlexity is O(v + e) as same as regular reversal, and uses a set to avoid revisiting. And the space comlexity is the set that stores all visited node, which is O(v).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public int shortestPath(List<GraphNode> graph, GraphNode start, GraphNode target) {
	if (graph == null) return -1;
	if (start == target) return 0;

	Queue<GraphNode> q = new LinkedList<>();
	Ser<GraphNode> visited = new HashSet<>();
	int step = 0;

	q.offer(start);
	visited.add(start);
	while (!q.isEmpty()) {
		int size = q.size();
		step += 1;
		for (int i = 0; i < size; i++) {
			GraphNode cur = q.poll();
			for (GraphNode nei : cur.neighbors) {
				if (nei == target) {
					return step;
				}
				if (!visited.contains(nei)) {
					q.offer(nei);
					visited.add(nei);
				}
			}
		}
	}
	return -1;
}

ShortestPath(bidirection)

input: List of graph node, starting node, and target node. If given graph is not null, both start and end position are not null.
output: Return the shortest path from the start to the target. If there is not such path, return -1.

step plus one from each direction.

In a regular traversal, the time comlexity is about the same as monodirection. And the space remains the same. It is beacuse, even though traversing from two direction “at the same time”, the total number of node in the graph is given.
However, if each node expends X states at a level, and there are N levels. Then the time complexity is going to be X^N. Coming from two directions will reduce level to N/2 for each direction. The the time comlexity becomes 2 * X^(N/2), which optimizes about squareroot of the complexity.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
public int shortestPath(List<GraphNode> graph, GraphNode start, GraphNode target) {
	if (graph == null) return -1;
	if (start == target) return 0;

	Queue<GraphNode> qStart = new LinkedList<>();
	Ser<GraphNode> visitedStart = new HashSet<>();

	Queue<GraphNode qTarget = new LinkedList<>();
	Ser<GraphNode> visitedTarget = new HashSet<>();

	int step = 0;

	qStart.offer(start);
	visitedStart.add(start);

	qTarget.offer(target);
	visitedTarget.add(target);

	while (!qStart.isEmpty() && !q.target.isEmpty()) {
		//from start
		int sizeStart = qStart.size();
		step += 1;
		for (int i = 0; i < sizeStart; i++) {
			GraphNode cur = qStart.poll();
			for (GraphNode nei : cur.neighbors) {
				if (qTarget.contains(nei)) return step;
				if (!visitedStart.contains(nei)) {
					qStart.offer(nei);
					visitedStart.add(nei);
				}
			}
		}
		//from target
		int sizeTarget = qTarget.size();
		step += 1;
		for (int i = 0; i < sizeTarget; i++) {
			GraphNode cur = qTarget.poll();
			for (GraphNode nei : cur.neighbors) {
				if (qStart.contains(nei)) return step;
				if (!visitedTarget.contains(nei)) {
					qTarget.offer(nei);
					visitedTarget.add(nei);
				}
			}
		}
	}

	return -1;
}

Onlything changed in bidirection traverse is adding a queue for the direction, and check whether current node expands a node in the queue of the other direction.